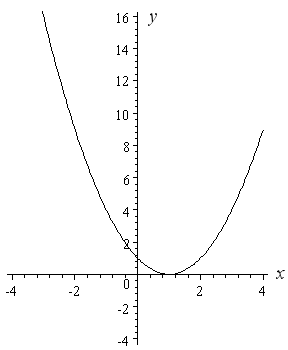
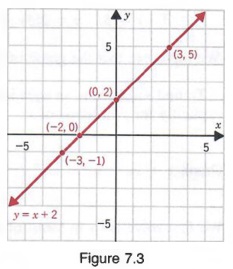
Graphing y = x 2 We have already discovered how to graph linear functions But what does the graph of y = x 2 look like?Solution Steps y = x2 y = x 2 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side x2=y x 2 = y Subtract 2 from both sides Subtract 2 from both sides11 Solve yx2 = 0 Tiger recognizes that we have here an equation of a straight line Such an equation is usually written y=mxb ("y=mxc" in the UK) "y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis In
How To Draw Y 2 X 2
Y x 2
Y x 2- Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign upFree quadratic equation calculator Solve quadratic equations using factoring, complete the square and the quadratic formula stepbystep



Function Y X 2 Geogebra
SOLUTION slope of, y=x^2 You can put this solution on YOUR website!Calculus Integral with adjustable bounds example Calculus Fundamental Theorem of CalculusHow to Check Your Answer with Algebra Calculator First go to the Algebra Calculator main page Type the following First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6
Polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2 Example 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2Y=x^2 WolframAlpha Volume of a cylinder?Click here👆to get an answer to your question ️ The range of the function y = x/1 x^2 is
Y=x2 (1,1) (4,2) Figure 2 The area between x = y2 and y = x − 2 split into two subregions If we slice the region between the two curves this way, we need to consider two different regions Where x > 1, the region's lower bound is the straight lineIt will strictly increase in those intervals where dxdy > 0 Now, dxdy = −x2e−x e−x(2x) = e−x(2x−x2) e−x will be always positive, so the function will strictly increase in those intervals where 2x−x2 > 0 The number line showing the sign of 2x−x2 is shown in the figure so the function will strictly increase in (0,2)This problem has been solved!



What Is The Equation Of Tangent And Normal To The Curve Y X2 1 At 1 2 Quora




Systems Of Equations With Graphing Article Khan Academy
Suppose the curves are x = y2 and x = 4 y2 and and you want to find points on the two curves with the same yvalue Then substitute y 2 from the first equation into the second to obtain x = 4 x So to achieve the same yvalue the xvalue on the second curve must be (minus) 4 times the xvalue on the first curve x = 4y2 and x = y2However, the converse is not in general true As a simple example, suppose that X X X is a standard normal random variable and that Y = X 2 Y = X^2 Y = X 2 Notice that knowledge of X X X completely determines Y Y Y, in which case X X X and Y Y Y are very clearly dependentLet's graph y=x 2 (blue), y=¼x 2 (green), y=½x 2 (purple), y=2x 2 (red), and y=4x 2 (black) on the same axes For all these positive values of a, the graph still opens up Notice when 0




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram




How To Graph Y Sqrt X Video Lesson Transcript Study Com
Simple and best practice solution for Y=x^240 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,We can do this because we are not multiplying by zero #1 First post for me, so if I'm breaking a rule be gentle If someone can point me to how to get the theta, pi, etc, symbols that would be great also y=x^2 rsin (theta)=rcos (theta)rcos (theta) rsin (theta)=r^2 x cos^2 (theta) At this point I'm kind of lost, maybe I went down the wrong path Help appreciated, Thanks and Regards



Quadratic Equation Wikipedia




Characteristics Of Parabolas College Algebra
0 Office_Shredder said (xy) 2 = x 2 2xy y 2 >= 0 You know that already So x 2 xy y 2 >= xy If x and y are both positive, the result is trivial If x and y are both negative, the result is also trivial (in both cases, each term in the summation is positive) When one of x or y is negative, xy becomes positiveFor these solutions to exist, the discriminant should not be a negative number First, we need to compute the discriminant Discriminant d=4 is greater than zero That means that there are two solutions Again, the answer is 0, 2Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts
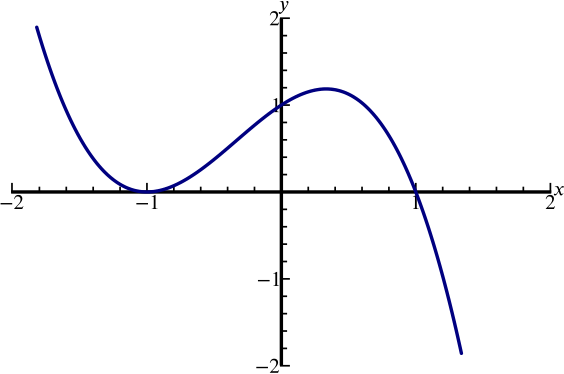



Can We Sketch The Graph Y X 3 X 2 X 1 Polynomials Rational Functions Underground Mathematics



Quadratics Graphing Parabolas Sparknotes
If you don't include an equals sign, it will assume you mean "=0" It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculations y = x 2 The yintercept is where the line crosses the yaxis So which ever graph has 2 as the yintercept in correctIts more complex when the graphs have the same intercept but in this case this should be easy to find So looking at the graphs you can see that the 3rd graph is the correct answer I hope this helps love!Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you




How To Draw Y 2 X 2
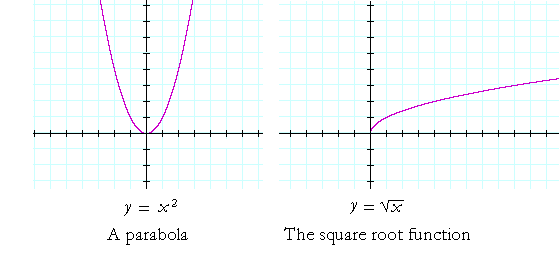



Graph Of A Parabola Topics In Precalculus
Graph y=x^2 Graph of a Parabola In mathematics, a quadratic equation is a polynomial equation in which the highest exponent of the independent variable is twoAs you can see, this is again a linear differential equation of the type dy/dx Py = Q, where Q is a function of x We rearrange the original DE to get dy/dx y = x^2 > 1 The Integrating Factor = e^(Integral of P dx) = ePiece of cake Unlock StepbyStep y=x^2 Extended Keyboard Examples
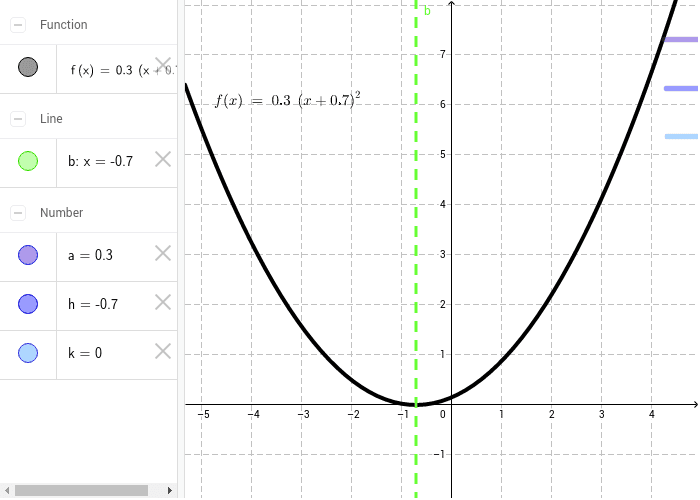



Transformations To The Graph Of Y X 2 Geogebra



Quadratics
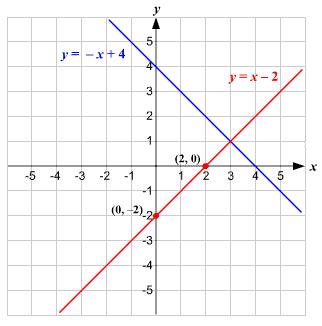
Exercise 811 Verify that y = 2e3x − 2x − 2 is a solution to the differential equation y′ − 3y = 6x 4 Hint First calculate y ′ then substitute both y ′ and y into the lefthand side It is convenient to define characteristics of differential equations that make it easier to talk about them and categorize themCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method y=3x4;y=x2 Tiger Algebra Solver



How Do You Graph The Line Y X 2 Example




Function Families Ck 12 Foundation
Free slope calculator find the slope of a line given two points, a function or the intercept stepbystepSOLUTION graph the quadritic equation y= x^2 2x Practice!Set y y equal to the new right side y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down
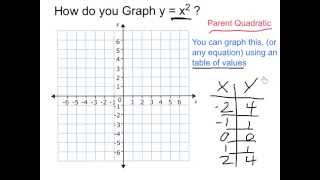



Graph Y X 2 Youtube




Hypot Wikipedia
Rewrite as x^22xy=0 This is a quadratic equation in variable x Don't be confused, I'm just pointing out that we will temporarily be thinking of y as a constant (a number) We would solve by factoring if we could, but we can't so we'll use the quadratic formula, which says that the solutions to 2x^2 bx c = 0 are x=(bsqrt(b^24ac))/(2a)Algebra Graph y=x2 y = x − 2 y = x 2 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x bYou can put this solution on YOUR website!
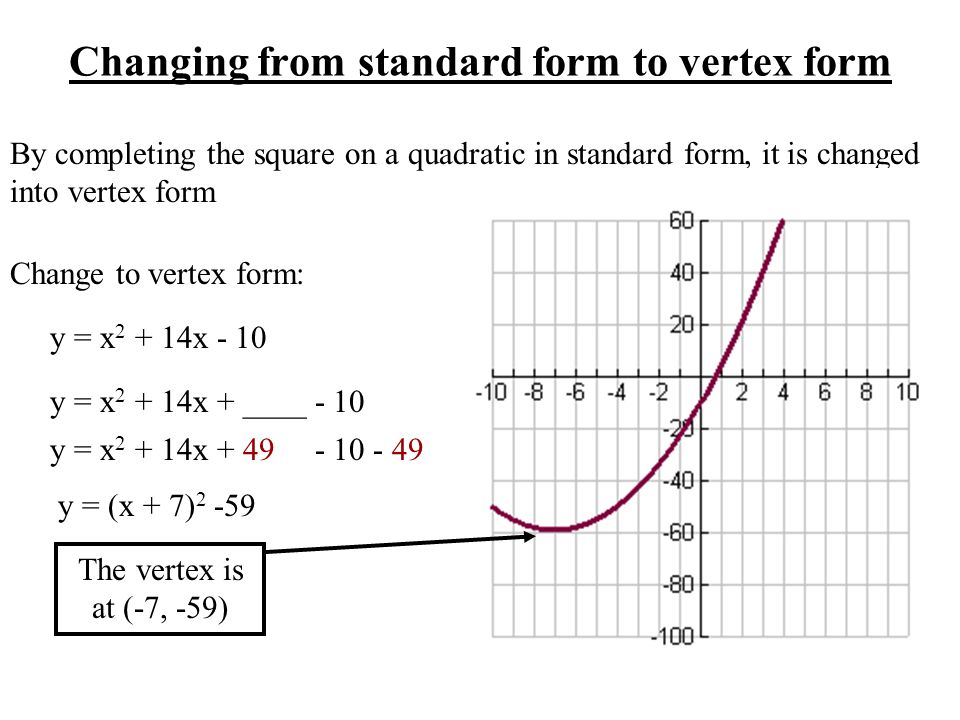



Completing The Square Ppt Video Online Download




Y X 2 1 Y 0 X 2 X 3 Novocom Top
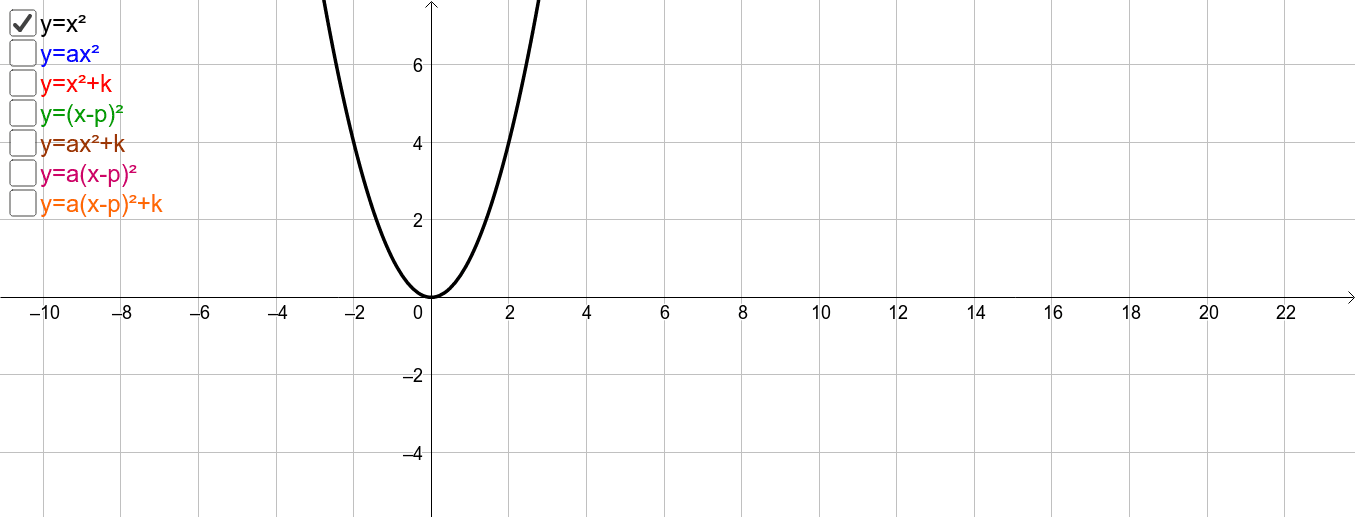
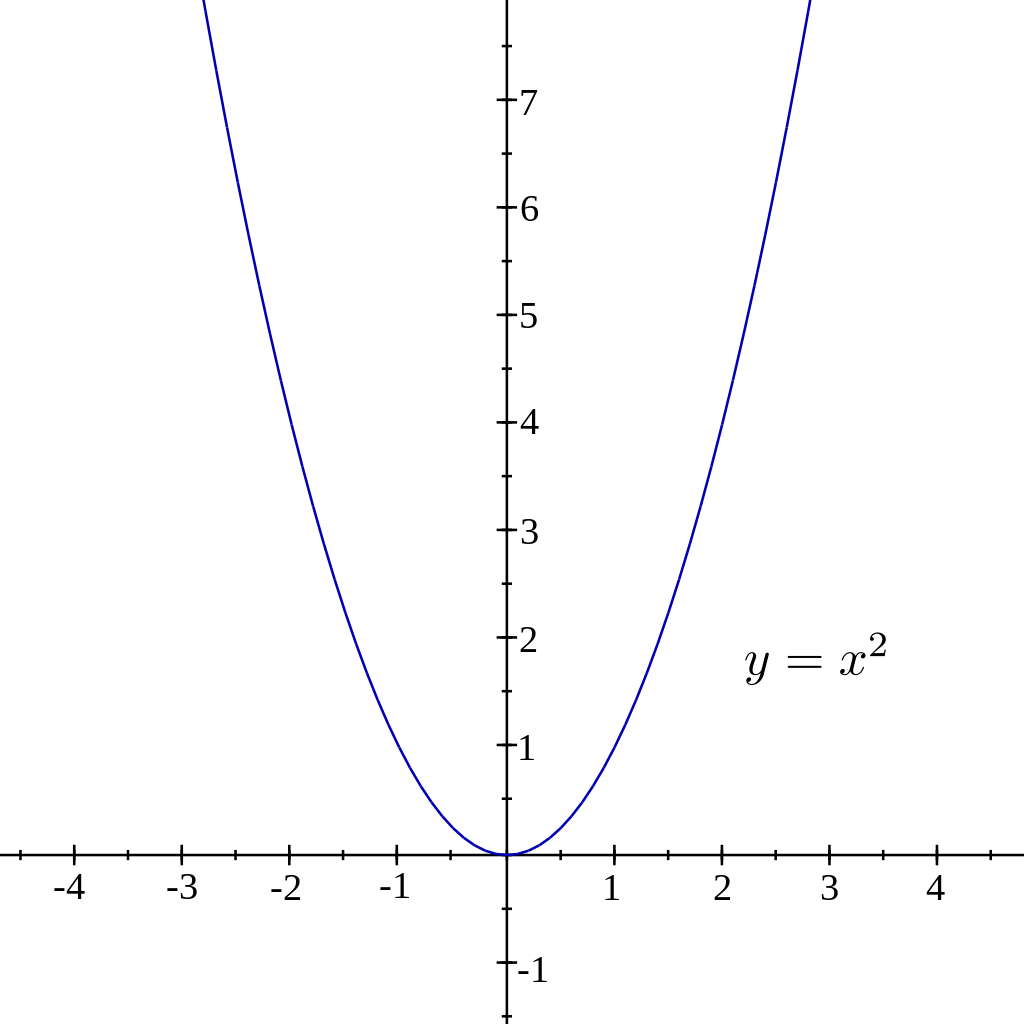
Y=X^2 Transformations Y=X^2 Transformations Log InorSign Up y = a bx − h 2 k 1 h = 0 2 k = 0 3 a = 1 4 b =Answer to Find the area of the region bounded y = x^2 5x 4, x = 2, y = 0 is revolved about the xaxis By signing up, you'll get thousands ofTo find the answer, make a data table Data Table for y = x 2 And graph the points, connecting them with a smooth curve Graph of y = x 2 The shape of this graph is a parabola Note that the parabola does not have a constant




Function Y X 2 Geogebra



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4
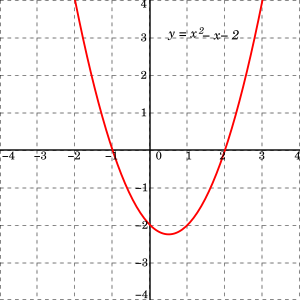
\(y = x^2 a\) represents a translation parallel to the \(y\)axis of the graph of \(y = x^2\) If \(a\) is positive, the graph translates upwards If \(a\) is negative, the graph translatesSolution Steps y = x2 y = x − 2 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side x2=y x − 2 = y Add 2 to both sides Add 2 to both sidesThe equation is a quadratic equation We can NOT readily find the slope (or rate of change) of this function like we can with a linear equation simply using Algebra In fact, there are an infinite amount of slopes at an infinite amount of points for this function



Parabolas



Quadratics Graphing Parabolas Sparknotes
Reason x/y y/x = 2 Given x≠0 and y≠0 Because then the original question would be dividing by zero xy≠0 Because neither factor is zero (xy) (x/y y/x) = (xy) 2 Multiply both sides of given equation by (xy);Y >1/2 x ySee the answer Solve the initial value problem y'= (x^2y^2)/ (xy) with y (2)=2 It should be a bernoulli equation I've attached a picture Show transcribed image text
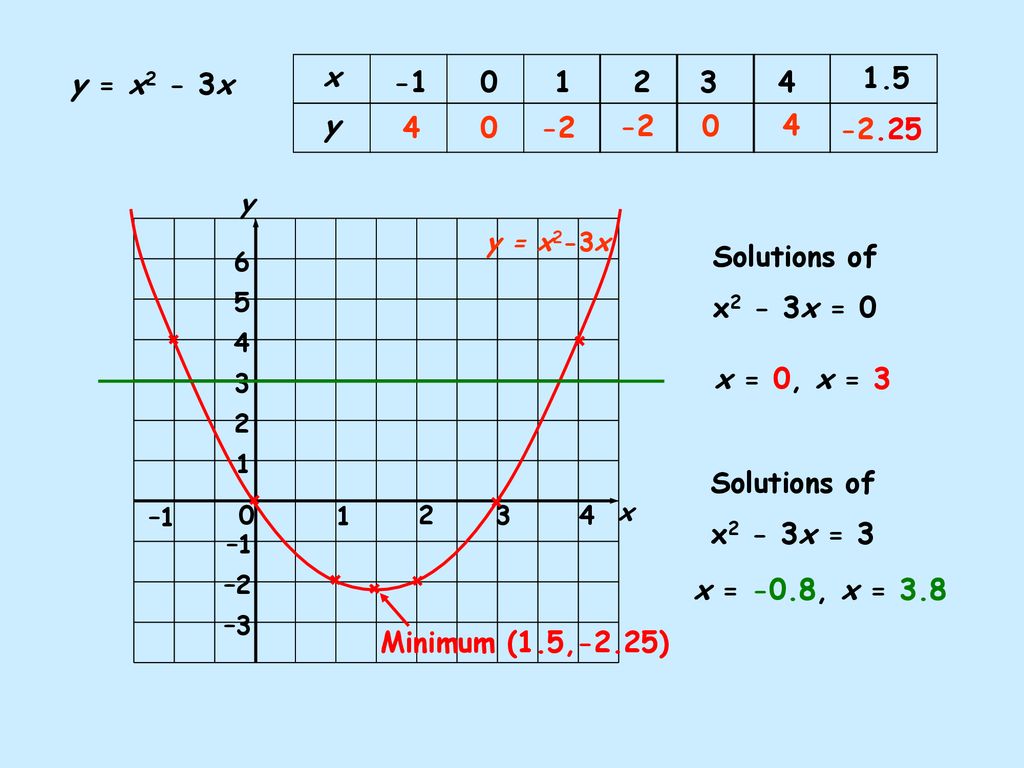



X Y Y X2 3x Solutions Of Y X2 3x Y X 1 5 2 3 6 Y X2 3x Ppt Download



Untitled Document
The operation occurs first, and its value is generated Its value is the value of x before the increment So that is what gets assigned to y The operation's side effect is that x is incremented, but that doesn't come into play when determining the expression's value Where as the x expression also has a value and a side effect Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be moved down by 2 units So we just take our first curve and move it down 2 units Our new curve's vertex is at −2 on the yaxisPLAY Match Gravity Which ordered pairs are in the solution set of the system of linear inequalities?




Graph Y X 2 3 Youtube



Graph Domain And Range Of Absolute Value Functions
2 Answers2 Your differential equation xy ′ − y = x2 can, assuming x ≠ 0, be rewritten as y ′ − 1 xy = x This is a first order differential question of the form y ′ P(x)y = Q(x) Such equations can be solved by finding an integrating factor, say μ, which when we multiply through by μ, the lefthand side is an exact derivative Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History




Content Transformations Of The Parabola




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
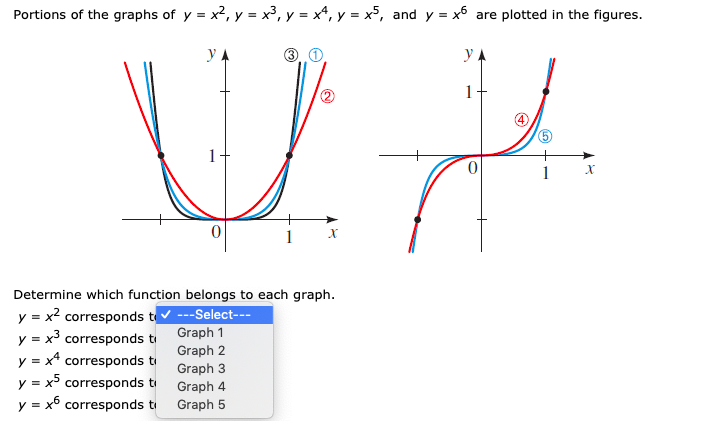



Portions Of The Graphs Of Y X2 Y X3 Y X Y X5 And Chegg Com



1
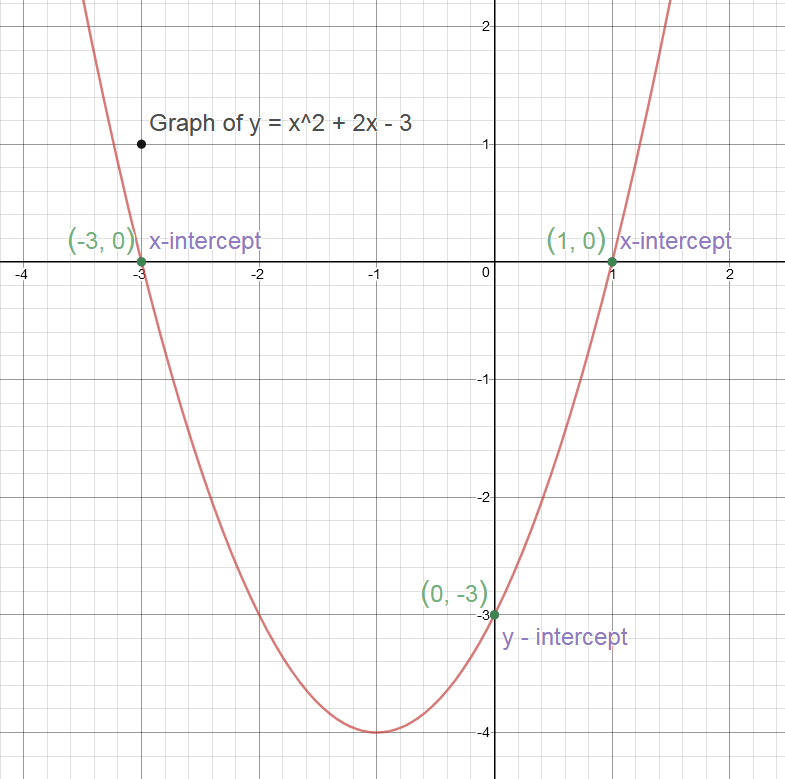



How Do You Find The X And Y Intercepts For Y X 2 2x 3 Socratic



Curve Shifting Because Of Addition Subtraction



Untitled Document




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Quadratic Function
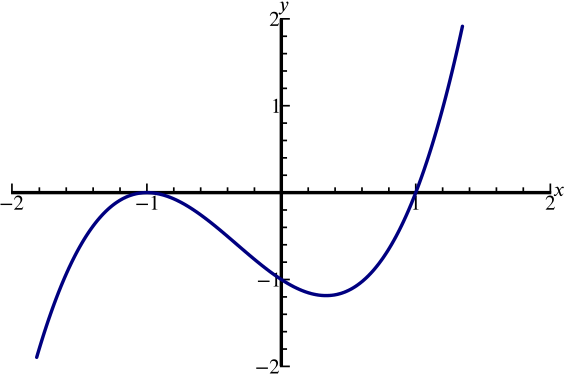



Solution Can We Sketch The Graph Y X 3 X 2 X 1 Polynomials Rational Functions Underground Mathematics
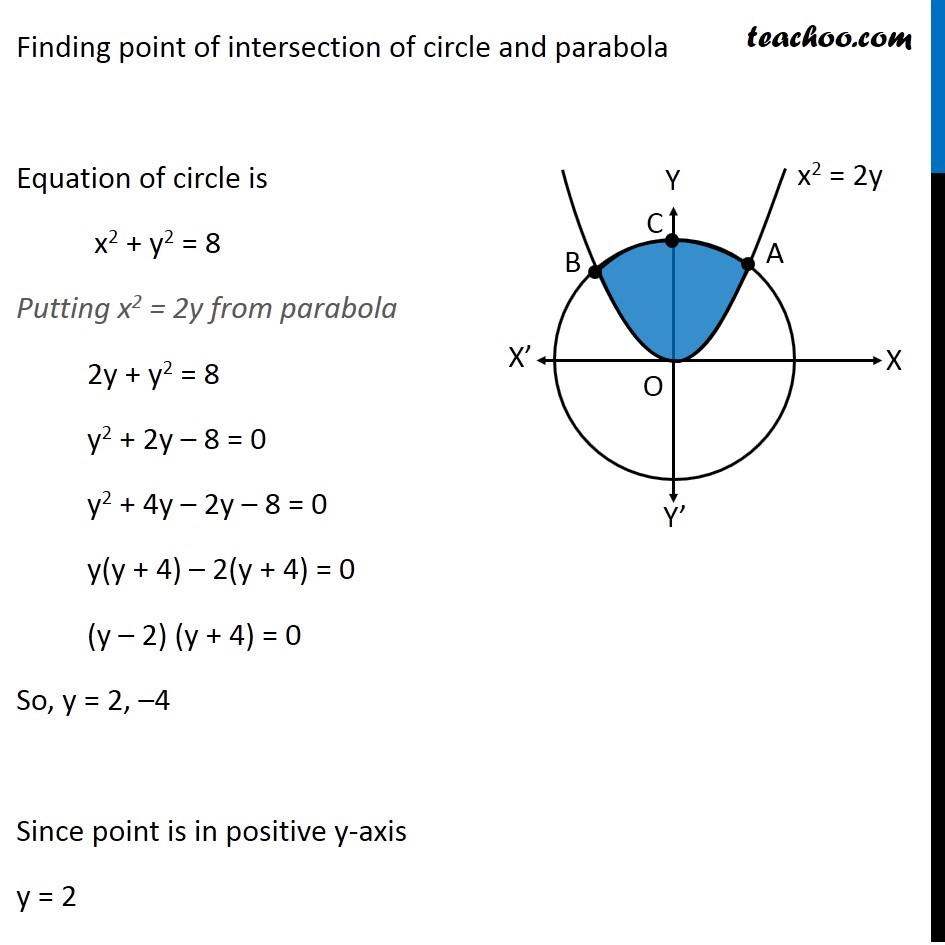



Find The Area Of The Region X Y X 2 Y 2 8 X 2 2y
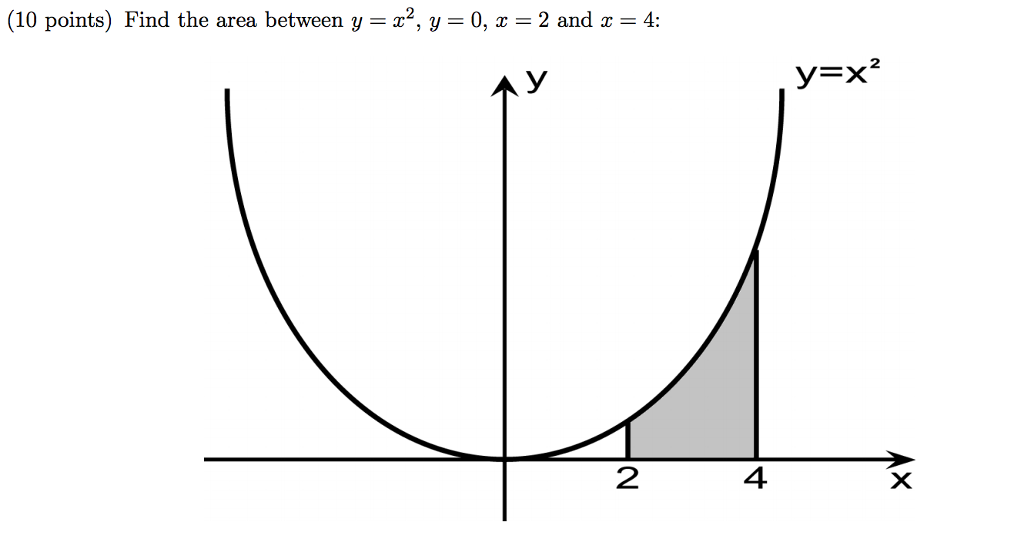



Find The Area Between Y X 2 Y 0 X 2 And X Chegg Com



How To Draw Y 2 X 2




What Is The Graph Of E X Quora



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4



Solution How Do You Graph Y X 2 And Y 2x 2




Algebra Calculator Tutorial Mathpapa



Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com
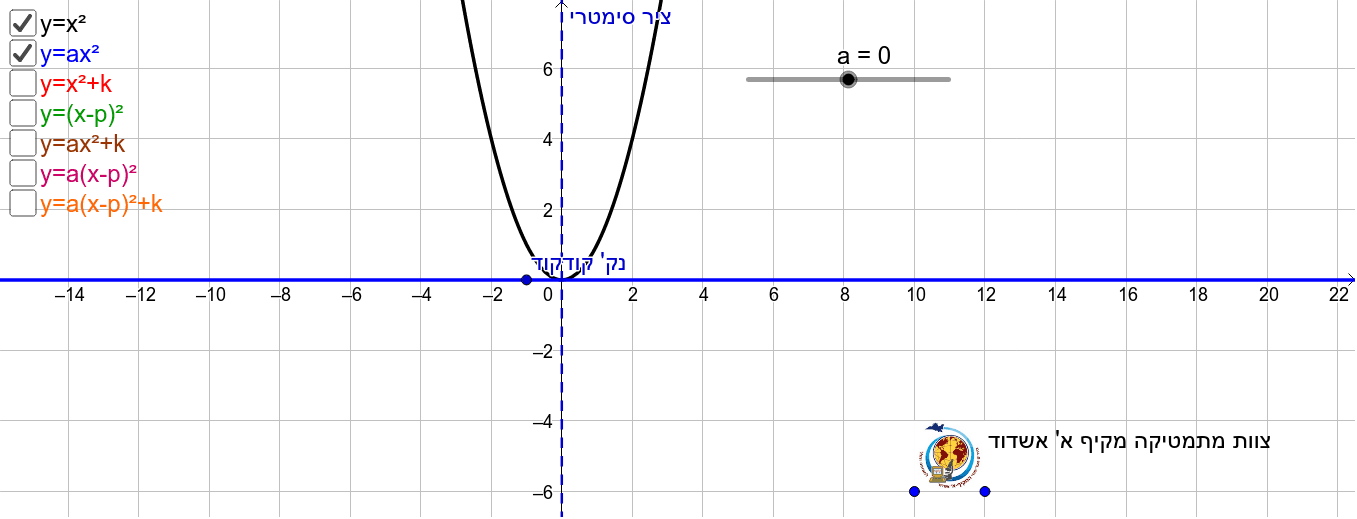



Parabola Y X 2 Geogebra
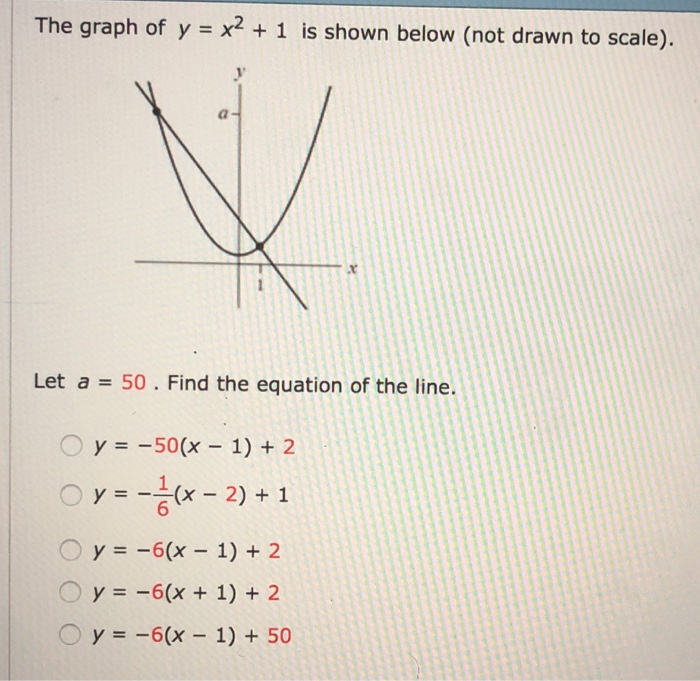



The Graph Of Y X2 1 Is Shown Below Not Drawn To Chegg Com
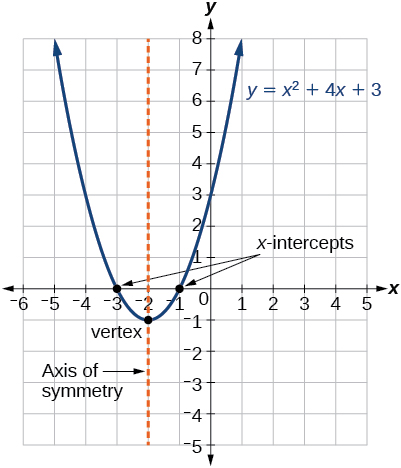



5 1 Quadratic Functions Mathematics Libretexts




Horizontal Line Test For Function To Have Inverse Expii



Finding Intercepts From An Equation



Y X 2 2
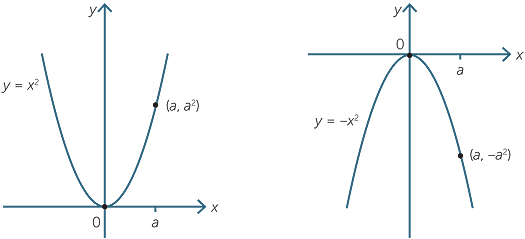



Quadratic Function



Solution 2 For The Function Y X2 4x 5 Perform The Following Tasks A Put The Function In The Form Y A X H 2 K Answer Show



Y X 2 2



Graph Graph Equations With Step By Step Math Problem Solver



Quadratics Graphing Parabolas Sparknotes



Curve Sketching



Move A Graph



File Y X 2 Svg Wikimedia Commons




Quadratic Function



Unique Quadratic Equation In The Form Y Ax 2 Bx C




How Do You Graph Y X 2 1 Socratic



Solve System Of Linear Equations Graphically




Graph Y X 2 Study Com



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora



Quadratics Polynomials Of The Second Degree Topics In Precalculus




Intro To Quadratic Graphs Key Features Of Parabolas Expii



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2



Y X 2 2




Graphing Parabolas




File Y X 2 2x Svg Wikimedia Commons
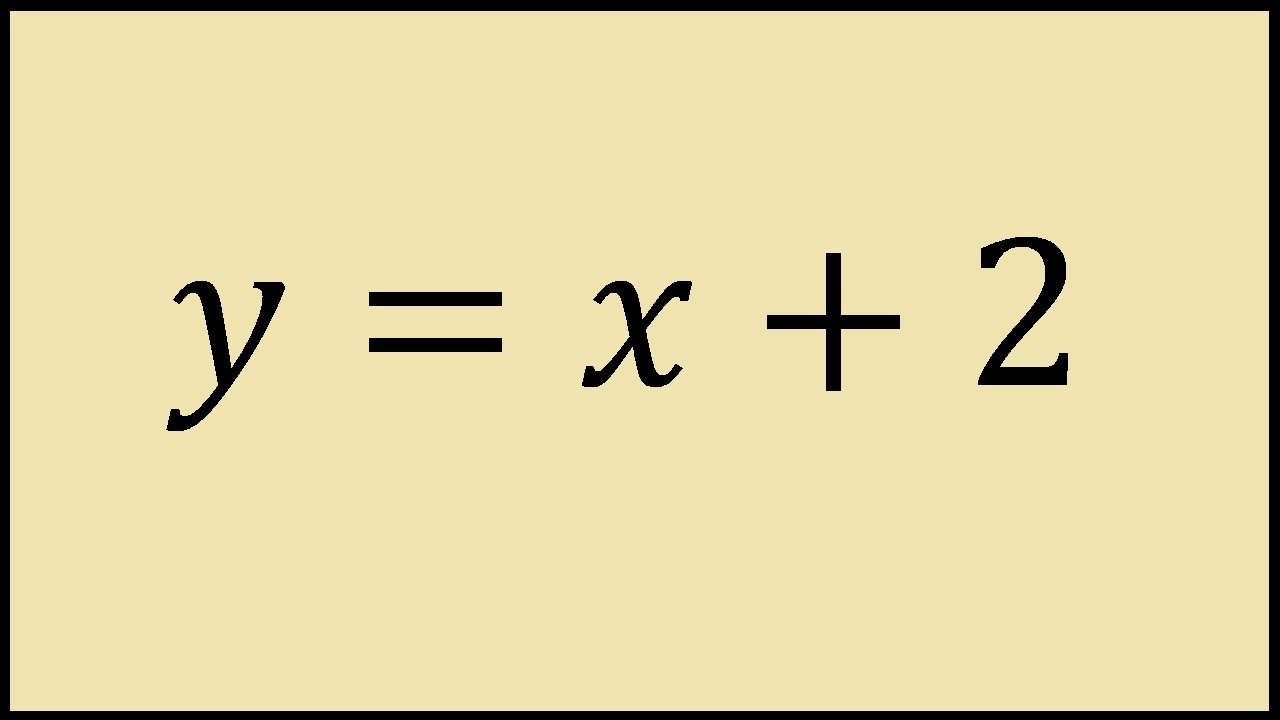



How To Graph Y X 2 Youtube
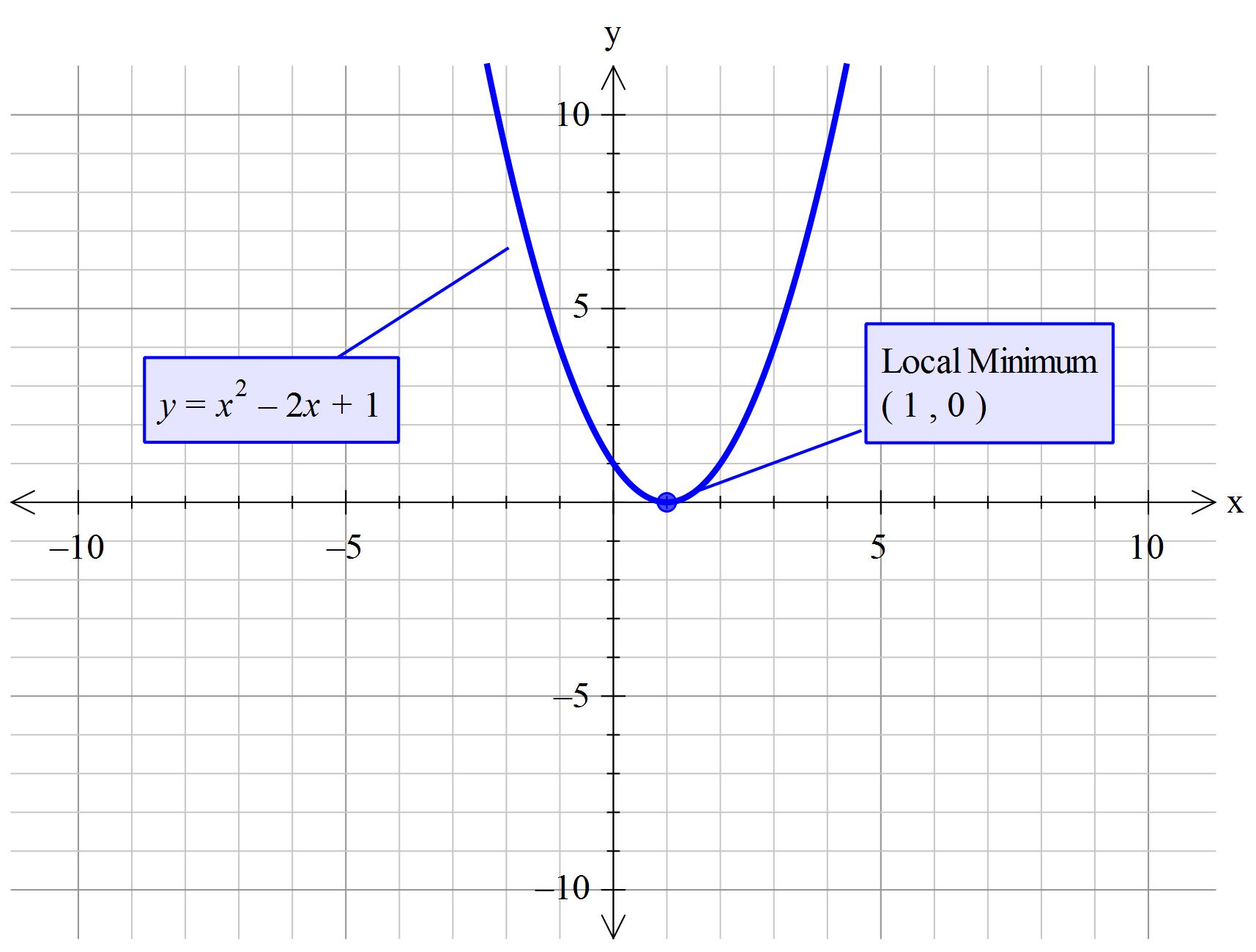



What Is The Vertex Of Y X 2 2x 1 Socratic




Scaling Reflecting Parabolas Video Khan Academy
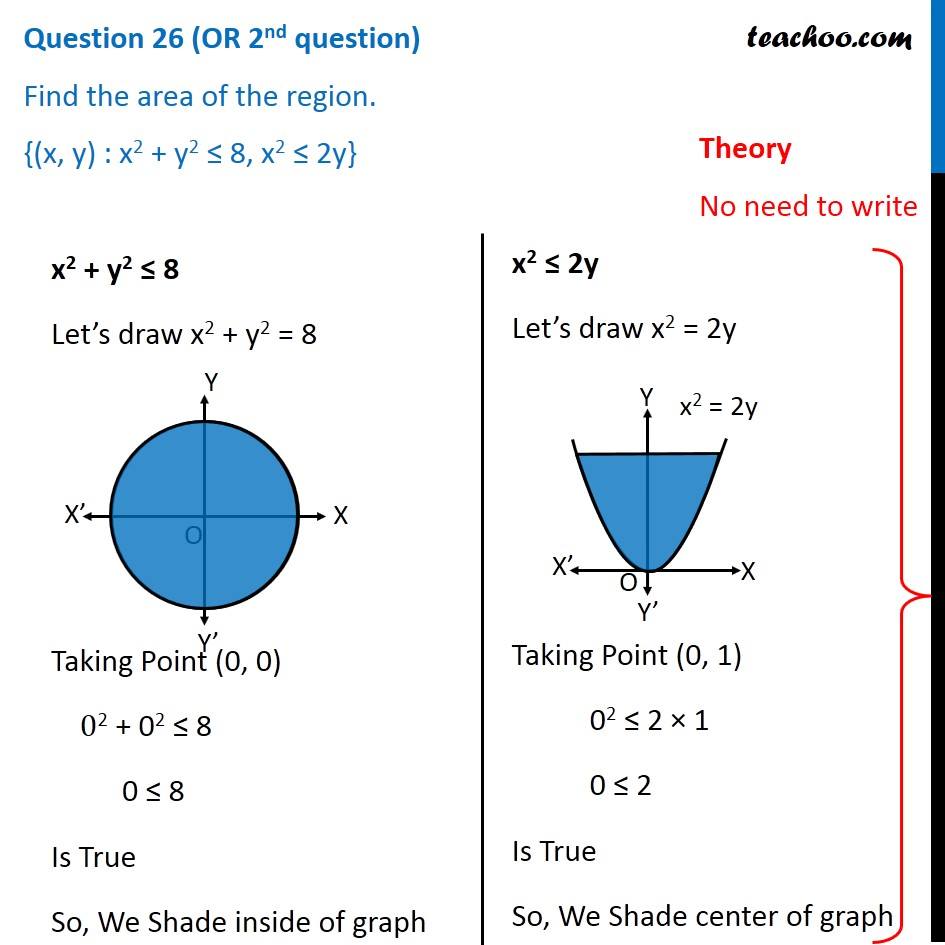



Find The Area Of The Region X Y X 2 Y 2 8 X 2 2y



Graph Graph Equations With Step By Step Math Problem Solver




Finding The X Intercepts Of A Function Math Bootcamps




Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube



1




Graphing Linear Inequalities



Solution Use The Graph Of Y X 2 2x 8 Does This Function Have A Maximum And Minimum And If So What Are They
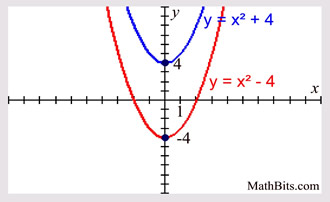



Parabola Parent Function Mathbitsnotebook Ccss Math



How Do You Graph The Line Y X 2 Example



Graph Y X 2 Youtube



Graphing Quadratic Functions
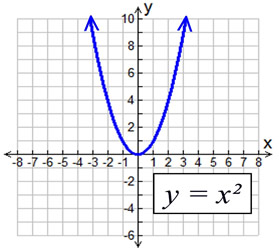



Parabola Parent Function Mathbitsnotebook Ccss Math
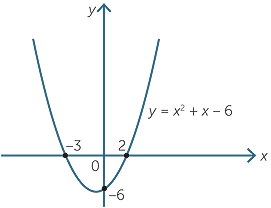



Quadratic Function




The Area Bounded By The Curve Y X 2 1 From X 2 To X 3 Emathzone
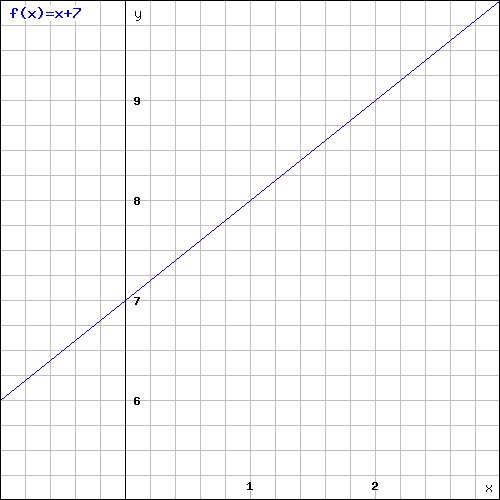



Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet



Graphing Quadratic Functions



Quadratics Graphing Parabolas Sparknotes




Learn About Reflection Over The Line Y X Caddell Prep Online



Quadratic Functions



1



Quadratics
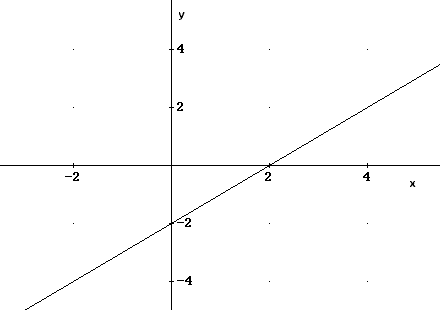



Graph Domain And Range Of Absolute Value Functions



Graphing Quadratic Functions
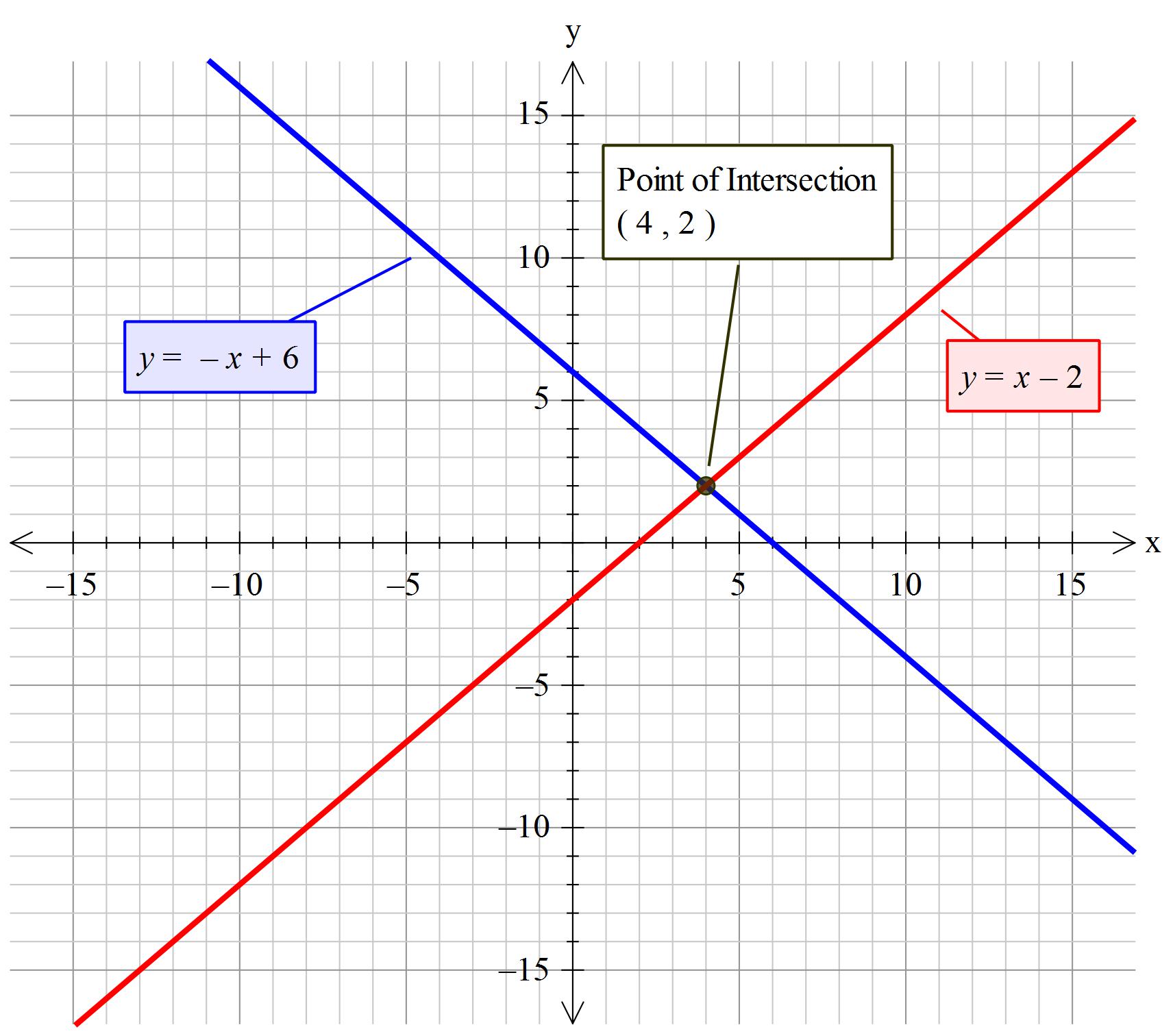



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic



Solution Describe The Change In Y X 2 For Each Equation Y X 6 2 The Phrase Quot Describe The Change Quot Confuses Me Is This The Same As Solving Should I Be Changing The Equation To




Transformations Of Quadratic Functions College Algebra




Example 15 Find Area X Y 0 Y X2 1 0 Y X 1



Search Q Y 3d X 5e2 Tbm Isch



Math Spoken Here Classes Quadratic Equations 3



Curve Shifting Because Of Addition Subtraction



Graph Of Standard Linear Relations Between X Y Graph Of Y X



0 件のコメント:
コメントを投稿